The methodology of this research facilities completely on deep studying methods to comprehensively forecast CO2 emissions from autos. The method started with preprocessing and information assortment, adopted by the creation of the MLP mannequin. Moreover, explainable AI (XAI) strategies, significantly Shapley Additive Explanations (SHAP), have been utilized to reinforce the interpretability and reliability of predictions. An summary of the methodology used on this research is proven in Determine 2.
This research’s dataset, which was obtained from Kaggle, offers intensive info on how CO2 emissions differ relying on varied car parameters. The dataset compiles information from the Canadian authorities’s official open information web site, spanning a interval of seven years Dataset. The dataset, which incorporates 12 columns and 7385 rows throughout a 7-year span is an intensive info supply. Data on car fashions, gasoline sorts, transmissions, metropolis and freeway gasoline consumption scores, and CO2 emission ranges is all included. Desk 2 presents an summary of the traits, explanations, and related values of the dataset.
The “uel Consumption Comb (mpg)” column within the dataset was initially added to signify gasoline consumption in miles per gallon (mpg). Nonetheless, extra evaluation revealed that the reported values didn’t match the conventional conversion from litres per 100 km (L/100 km) to miles per gallon (mpg)51. The proper conversion method is as follows:
$$start{aligned} textual content {mpg} = frac{235.215}{L / 100 Km} finish{aligned}$$
(1)
As a result of disparity between the reported “Gasoline Consumption Comb (mpg)” values and the anticipated values estimated utilizing the conversion process, this column was faraway from the dataset. As a substitute, the column reflecting gasoline utilization in litres per 100 km (L/100 km) shall be used for added evaluation and modelling.
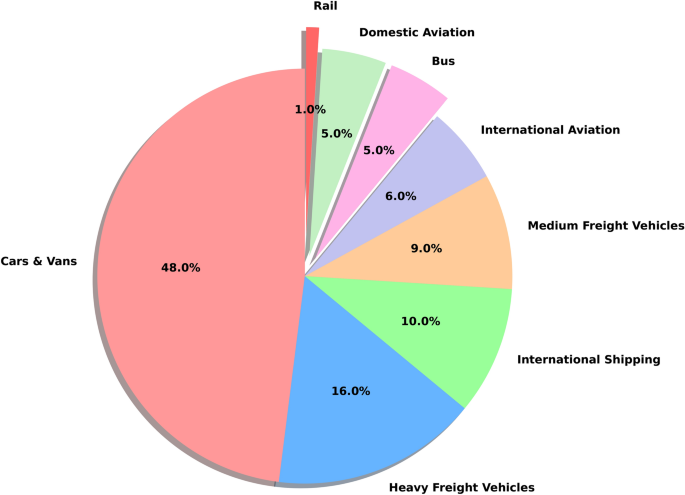
A definite sample emerged from the evaluation of CO(_2) emissions by car mannequin: autos with high-performance engines, corresponding to SRT, Rolls Royce, and Lamborghini, had the best emissions, whereas fuel-efficient fashions, corresponding to Good and Honda, exhibited the bottom emissions. This commentary is per the speculation that giant engines produce extra CO(_2).
To quantify these observations, we calculated the imply CO(_2)emissions for 41 distinct automotive fashions displayed within the visualization. The imply was estimated by grouping the dataset by car maker and making use of the next formula52:
$$start{aligned} textual content {Imply CO}_{2} textual content { Emissions } = frac{1}{n} sum _{i=1}^{n} textual content { CO }_{2i} finish{aligned}$$
(2)
the place (n) represents the whole variety of entries for a particular car mannequin, and (textual content {CO}_{2i}) denotes the CO(_2) emissions for every entry.
This evaluation, illustrated in Determine 3, offers insightful info on how car design influences the environmental affect and underscores the significance of contemplating emissions in function choice for predictive evaluation.
The distribution of autos manufactured by every firm was skewed when analyzing the dataset collected over a interval of seven years in Canada. Ford had the best variety of vehicles (623); nonetheless, its common CO2 emissions have been comparatively average. This distinction highlights that whereas Ford’s giant car rely (623 vehicles (instances) 270 g/km/automotive = 168,210 g/km CO2 emissions) considerably contributes to complete emissions, it doesn’t consequence within the highest common emissions per car. In distinction, SRT had the fewest vehicles within the dataset, whereas Chevrolet was the second-largest producer when it comes to car rely. Determine 4 offers an summary of the variety of autos produced by every producer, demonstrating their contributions to total CO2 emissions.
The evaluation of the gasoline utilization developments for varied gasoline sorts revealed some notable patterns, as proven in Determine 5. Among the many gasoline sorts, ethanol (denoted as “E”) exhibited the best gasoline consumption. This elevated consumption could also be attributed the decrease vitality density of ethanol in comparison with that of gasoline. In distinction, fuels labelled “X” (common gasoline), “Z” (premium gasoline), and “D” (diesel) demonstrated decrease gasoline consumption ranges. Though pure gasoline, represented by “N”, is included within the dataset, just one car utilized this gasoline, and subsequently it’s not prominently displayed in Determine 6 on account of its restricted illustration.
Determine 6 illustrates that regardless of the upper gasoline consumption of ethanol, its CO2 emissions are akin to these of different fuels, significantly gasoline and diesel. This means that whereas ethanol might require extra gasoline per kilometer, it doesn’t produce proportionally greater CO2 emissions. Most autos within the dataset emit CO2 within the vary of 200 to 300 g/km, no matter gasoline sort, with ethanol barely overlapping this vary.
A abstract of the CO2 emissions dataset proven in Desk 3 is offered utilizing descriptive statistics. Vital particulars together with the engine measurement (ES) litres, variety of cylinders, gasoline consumption (FC) in metropolis, freeway, mixture (litres per 100 km), CO2 emissions (grams per kilometer), and the whole variety of observations are listed within the desk. As we will see, there’s a customary deviation of 1.35 litres and a median engine measurement of three.16 litres. A wide range of engine sizes, starting from 0.9 litres to eight.4 litres, are additionally proven by the statistics. This desk additionally offers info on the variations in CO2 emissions and gasoline utilization between the completely different vehicles. This synopsis establishes the framework for added investigation into the variables impacting CO2 emissions.
Attention-grabbing developments have been discovered by analyzing the hyperlinks between the options (aside from the article options) utilizing the correlation heatmap in Determine 7. Engine measurement demonstrates a sturdy constructive correlation with cylinder rely (0.93), and a reasonably sturdy correlation with gasoline consumption measures: metropolis (0.83), freeway (0.75), and mixed (0.81), in addition to CO2 emissions (0.85). This means that bigger engines with extra cylinders (0.93) usually result in greater gasoline consumption, with metropolis consumption exhibiting the strongest affiliation. Moreover, autos with greater metropolis gasoline consumption usually have greater freeway and mixed gasoline consumption, as demonstrated by the excessive correlations between these measures (all above 0.94). This reinforces the concept higher gasoline consumption throughout metropolis driving is related to greater consumption on highways and total. Correlation evaluation was carried out utilizing Python, with Pandas for information dealing with and Seaborn for producing the heatmap.
Knowledge pre-processing is a vital step in any deep studying modelling, because it immediately impacts the standard of the mannequin’s predictions. On this research, we carried out a complete and methodical pre-processing section to make sure that the dataset was clear, structured, and prepared for evaluation. Pre-processing includes dealing with lacking values, remodeling variables, addressing outliers, and getting ready the info for the deep studying pipeline. The objective of this course of was to remove any inconsistencies or anomalies which may hinder the mannequin’s efficiency. The pre-processing workflow concerned a number of key steps, that are outlined under:
Lacking and null values: Lacking or null values within the dataset can result in bias or inaccuracies in mannequin coaching, particularly when necessary variables are incomplete. The dataset was checked for each the values.
Duplicate Values: Duplicate information within the dataset can skew outcomes, resulting in incorrect mannequin outcomes by over-representing sure observations. A radical examine was carried out to establish any duplicate rows. After figuring out whether or not any entries within the information have been duplicates, values have been eradicated. This prevents the evaluation from being skewed and ensures that every information level represents a definite commentary.
Knowledge engineering is essential for enhancing the predictive functionality of deep studying fashions. In our research, we used a wide range of methods to arrange and modify the dataset, making certain that the mannequin might precisely forecast CO2 emissions based mostly on completely different car options.The next strategies have been utilized to arrange the dataset:
Outlier Detection and Elimination: Outliers have been recognized utilizing z-score evaluation and eradicated from the dataset. This section is essential for avoiding skewed mannequin predictions induced by excessive values that would have an effect on the training course of. Knowledge factors with a z-score higher than 2.6 have been declared outliers and eradicated, making certain that the mannequin was educated on clear information.
$$start{aligned} z_i = frac{x_i – mu }{sigma } finish{aligned}$$
(3)
The place (x_i) is a person information level, (mu) is the imply of the info, and (sigma) is the usual deviation.
Categorical Characteristic Encoding: To remodel categorical variables (corresponding to make, mannequin, car class, transmission, and gasoline sort) into numerical representations appropriate for the mannequin, we first used one-hot encoding. This strategy divides every class into binary columns, permitting the mannequin to successfully study from these variables. Nonetheless, we additionally assessed goal encoding, which calculates the imply goal worth for every class and replaces it with imply values. Though goal encoding can cut back dimensionality, we found that one-hot encoding improved the interpretability of the SHAP values in our fashions.
Normalization and Scaling: To make sure that each function contributes equally to the mannequin’s efficiency, the numerical options have been min-max scaled. This scaling methodology converts every function to a standard vary (0 to 1), thereby decreasing the affect of various items and magnitudes. This was significantly essential for options corresponding to gasoline consumption and engine measurement, which had completely different scales. The equation for min-max scaling is:
$$start{aligned} x_{textual content {scaled}} = frac{x – x_{textual content {min}}}{x_{textual content {max}} – x_{textual content {min}}} finish{aligned}$$
(4)
the place (x_{textual content {max}}) and (x_{textual content {min}}) are the minimal and most values, respectively.
In abstract, the info engineering course of was thorough and aimed toward enhancing the predictive capabilities of the mannequin. By detailing the strategies used for information preparation and their resultant results on the dataset, we offer a clearer understanding of how these methods contribute to total evaluation and modelling efforts.
The efficiency and robustness of the mannequin have been rigorously assessed on this research utilizing a 5-fold cross-validation method. This strategy efficiently generalizes the mannequin to unseen information, decreasing the potential of overfitting and enhancing the accuracy of our findings. The dataset was systematically partitioned into 5 equal sections, denoted as (D_1, D_2, D_3, D_4,) and (D_5). In every iteration of the cross-validation course of, 4 of those sections have been used for coaching the mannequin and the remaining part served because the validation set. This course of may be mathematically represented as follows:
$$start{aligned} textual content {Coaching Set} = D_{i} quad textual content {for} quad i in {1, 2, 3, 4, 5} finish{aligned}$$
(5)
$$start{aligned} textual content {Validation Set} = D_{j} quad textual content {for} quad j in {1, 2, 3, 4, 5}, quad j ne i finish{aligned}$$
(6)
This cross-validation process was repeated 5 instances to make sure that every subset was used as soon as because the validation set. The general course of is summarized as follows:
1.
Iteration 1:
Coaching on (D_2, D_3, D_4, D_5)
Validation on (D_1)
2.
Iteration 2:
Coaching on (D_1, D_3, D_4, D_5)
Validation on (D_2)
3.
Iteration 3:
Coaching on (D_1, D_2, D_4, D_5)
Validation on (D_3)
4.
Iteration 4:
Coaching on (D_1, D_2, D_3, D_5)
Validation on (D_4)
5.
Iteration 5:
Coaching on (D_1, D_2, D_3, D_4)
Validation on (D_5)
The 5-fold cross-validation methodology offers a extra legit estimate of mannequin generalization by testing a number of information partitions, thereby decreasing the potential for overfitting. By averaging the efficiency metrics throughout all 5 iterations, we comprehensively evaluated the efficiency of the mannequin. This strategy ensures that the findings are usually not unduly influenced by a particular train-test cut up, providing a extra dependable evaluation of the mannequin’s predictive capabilities.
Deep studying is a subset of machine studying that makes use of synthetic neural networks and is a helpful methodology for locating intricate patterns and relationships in data53. Deep studying fashions are distinct from typical machine-learning algorithms in that they’re composed of quite a few layers of interconnected neurons, which permits them to routinely extract significant options from uncooked data54. Deep studying fashions may be particularly helpful in CO2emission prediction due to their capability to handle non-linear correlations between car options and emissions. Owing to their multi-layered structure, deep studying fashions can seize these sophisticated interactions extra effectively than conventional machine studying fashions, which makes it tough to deal with such complexities55. A wide range of deep studying architectures are applicable for regression issues corresponding to CO2emission prediction56. This part presents the proposed structure and its improvement procedures.
This research launched a novel strategy for predicting CO2 emissions from car attributes. We constructed a light-weight deep studying mannequin utilizing a multilayer perceptron (MLP) structure. MLPs, that are neural community foundations, are composed of interconnected neuronal layers. This methodology harnesses the ability of deep studying to establish intricate connections between enter options and the goal variable (CO2 emissions).
Enter Format: The enter information for the proposed deep studying mannequin consists of a dataset with a number of options associated to car attributes, as described in Desk 2. These options embody attributes corresponding to Make (car producer), Mannequin, Car Class (VC), Engine Measurement (ES), Cylinders, and Gasoline Sort (FT), together with varied measures of gasoline consumption metropolis (FCCity), gasoline consumption freeway (FCH), and gasoline consumption mixed (FCcomb).
On this research a number of densely related layers have been used, every with ReLU activation for non-linearity. The design consists of an enter layer, three hidden layers with 128, 64, and 32 neurons every, and a single regression (linear activation) neuron within the remaining output layer.
The mannequin was constructed utilizing the Adam optimizer, which is a extremely environment friendly software identified for its effectiveness, particularly in large-scale fashions. The imply squared error (MSE) loss operate can be employed. The design was facilitated utilizing TensorFlow’s Keras Utility Programming Interface (API). Determine 8 offers a visible illustration of the structure of the proposed deep studying mannequin.
The objective of the proposed mannequin is to forecast CO2 emissions utilizing the offered dataset. In its formulated type, the mannequin structure is:
$$start{aligned} textual content {Enter:} quad x_{textual content {prepare}} quad (textual content {form: } (n,m)) finish{aligned}$$
(7)
$$start{aligned} start{aligned}&textual content {Hidden 1:} quad h^{(1)} = textual content {ReLU} left( x_{textual content {prepare}} cdot W^{(1)} + b^{(1)} proper) &qquad qquad qquad qquad qquad (textual content {form: } (n, 128)) finish{aligned} finish{aligned}$$
(8)
$$start{aligned} start{aligned}&textual content {Hidden 2:} quad h^{(2)} = textual content {ReLU} left( h^{(1)} cdot W^{(2)} + b^{(2)} proper) &qquad qquad qquad qquad qquad (textual content {form: } (n, 64)) finish{aligned} finish{aligned}$$
(9)
$$start{aligned} start{aligned}&textual content {Hidden 3:} quad h^{(3)} = textual content {ReLU} left( h^{(2)} cdot W^{(3)} + b^{(3)} proper) &qquad qquad qquad qquad qquad (textual content {form: } (n, 32)) finish{aligned} finish{aligned}$$
(10)
$$start{aligned} start{aligned}&textual content {Output:} quad Y_{textual content {pred}} = h^{(3)} cdot W^{(4)} + b^{(4)} &qquad qquad qquad qquad qquad (textual content {form: } (n, 1)) finish{aligned} finish{aligned}$$
(11)
Within the given neural community structure, the whole course of from enter to output may be traced by way of a number of equations, every detailing a particular layer or operation. The enter layer outlined in Equation (7), makes use of the coaching information (x_{textual content {prepare}}) which has (n) samples and (m) options. Equation (8) describes the primary hidden layer (h^{(1)}) the place the ReLU activation operate is employed after combining the inputs with weights (W^{(1)}) and biases (b^{(1)}). Additional transformations occurred in subsequent hidden layers. The second hidden layer (h^{(2)}) is represented by Equation (9), once more utilizing the ReLU operate. Nonetheless, the outputs from the primary hidden layer are processed with a brand new set of weights (W^{(2)}) and biases (b^{(2)}). The third hidden layer adopted the same sample, as detailed in Equation (10), processing the output of the second hidden layer utilizing the weights (W^{(3)}) and biases (b^{(3)}). The community output (Y_{textual content {pred}}), which predicts (textual content {CO}_2) emissions, was calculated utilizing Equation (11). This output is the results of processing the activation of the third hidden layer utilizing the ultimate set of weights (W^{(4)}) and biases (b^{(4)}). Every step depends on weights (W^{(i)}) and biases (b^{(i)}) for every layer, driving ahead the community’s potential to study and make correct predictions based mostly on enter information.
Our deep studying mannequin underwent intensive fine-tuning utilizing varied hyperparameters to make sure dependable and constant CO(_2) emissions forecasts. After evaluating the a number of configurations, we recognized the optimum settings for the proposed structure. The chosen design employs ReLU activation for non-linearity and consists of three hidden layers hanging an efficient stability between effectivity and complexity. The Imply Squared Error (MSE) loss operate aligns nicely with our regression targets, whereas the Adam optimizer enhances coaching effectivity.
To be able to mitigate overfitting, the mannequin was educated for 100 epochs with a batch measurement of 8, utilizing a 5-fold cross-validation strategy to make sure efficient studying from the info. These rigorously chosen hyperparameters considerably improved the robustness and accuracy of the mannequin in predicting CO(_2) emissions. Desk 4 offers a complete overview of the methods employed to optimize efficiency, detailing the varied hyperparameters concerned within the mannequin optimization course of.
explainable AI (XAI) strategies are designed to reinforce the interpretability of fashions and supply insights into the weather that affect predictions. On this research, we employed strong XAI methods, particularly SHapley Additive exPlanations (SHAP), to realize perception into the affect of options on CO2 emission projections. We used a sequence of visualizations, together with SHAP Abstract, waterfall, pressure, and dependence plots.
The SHAP values provide a sturdy framework for explaining particular person predictions by quantifying the contribution of every the (i^textual content {th}) function to the output of the mannequin. The SHAP worth for function is calculated utilizing the next equation:
$$start{aligned} SHAP_i = phi _0(f) + sum _{j=1}^{M} frac{(M-j)! cdot j!}{M!} left( phi _j(f) – phi _{j-1}(f) proper) finish{aligned}$$
(12)
the place; (SHAP_i) represents the SHAP worth for the (i^textual content {th}) function, (phi _0(f)) denotes the baseline contribution of the mannequin output, (f) is the proposed CarbonMLP mannequin that maps the enter options to the anticipated CO2 emissions, (M) is the whole variety of options.
To calculate the contribution of the options, the SHAP methodology considers all potential mixtures of function values and their respective outputs, offering a good distribution of the mannequin’s prediction among the many enter options. Which means that every function’s contribution is evaluated within the context of all different options, making certain that the interactions are correctly accounted for. The options used on this research and their descriptions are listed in Desk 2. These embody attributes corresponding to make (car producer), Mannequin, Car Class, Engine Measurement, Cylinders, and Gasoline Sort, in addition to varied measures of gasoline consumption (metropolis, freeway, mixed), that are important to understanding how car traits have an effect on CO2 emissions. The SHAP worth explains the affect of every function on mannequin output predictions. SHAP values not solely quantify the contributions of particular person options but in addition enable for a deeper understanding of how car traits affect (hbox {CO}_{{2}}) emission predictions. This technique enhances mannequin transparency and aids stakeholders in making knowledgeable selections based mostly on evaluation.
The SHAP abstract plot offers a world view of the significance of the imply absolute SHAP worth of every function. This helps with mannequin interpretation and validation by enabling the identification of necessary predictors and their specific results on mannequin predictions. In Equation (13), The place (N) represents the variety of options. The plot was calculated as follows:
$$start{aligned} textual content {SHAP Abstract Plot}=sum _{i=1}^{N} |SHAP_i |finish{aligned}$$
(13)
The SHAP waterfall plot reveals how every function contributes to the variation within the base worth, offering detailed insights into particular person predictions. This makes it simpler to interpret sure forecasts by emphasizing the variables that affect mannequin outputs and potential areas for improvement. In Equation (14), is calculated as follows:
$$start{aligned} textual content{ SHAP } textual content{ Waterfall } textual content{ plot }=textual content {Base Worth} + sum _{i=1}^{N} SHAP_i finish{aligned}$$
(14)
The SHAP pressure plot illustrates how every attribute impacts a single prediction, and reveals how the mannequin determines the output for a given occasion. This enables function impacts to be examined, highlighting how every contributes to the ultimate prediction and improves mannequin transparency. In Equation (15), is calculated for the pressure plot as:
$$start{aligned} textual content{ SHAP } textual content{ Power } textual content{ plot }=textual content {Base Worth} + sum _{i=1}^{N} SHAP_i finish{aligned}$$
(15)
The SHAP dependence plot considers the relationships with different variables and reveals the connection between a function and the mannequin output forecast. It offers necessary insights into the function habits and mannequin efficiency by helping within the discovery of advanced patterns and nonlinear relationships. The plot was calculated utilizing Equation (16):
$$start{aligned} Output Prediction = textual content {f(x)}+ sum _{i=1}^{N} SHAP_i finish{aligned}$$
(16)
Analysis metrics are essential for evaluating the effectiveness and efficiency of predictive fashions in sensible purposes. This element contained the metrics used to evaluate the efficiency of the proposed mannequin. The metrics included the Imply Squared Error (MSE), Root Imply Squared Error (RMSE), R-squared (R2), and Imply Absolute Share Error (MAPE).
The efficacy of the mannequin was assessed utilizing Imply Squared Error (MSE), which measures the common squared distinction between the anticipated and noticed outcomes. This calculation is expressed by the next equation:
$$start{aligned} textual content {MSE} = frac{1}{n} sum _{i=1}^{n} (y_i – hat{y}_i)^2 finish{aligned}$$
(17)
the place, (n) are the variety of samples, (y_i) represents the goal worth, and (hat{y}_i) denotes the goal worth, respectively.
The sq. root of the Imply Squared Error (MSE), also referred to as the Root Imply Sq. Error (RMSE), is the imply distinction between the noticed and predicted outcomes. The RMSE was calculated as follows :
$$start{aligned} textual content {RMSE} = sqrt{frac{1}{n} sum _{i=1}^{n} (y_i – hat{y}_i)^2} finish{aligned}$$
(18)
The R-squared (R(^2)) statistic illustrates the extent to which the impartial variables account for the variance within the dependent variable. On the size, which works from zero to at least one, greater numbers denote a greater mannequin match.The R(^2) method is as follows:
$$start{aligned} R^2 = 1 – frac{sum _{i=1}^{n} (y_i – hat{y}_i)^2}{sum _{i=1}^{n} (y_i – bar{y})^2} finish{aligned}$$
(19)
the place, (bar{y}) represents the imply of the noticed values.
The common share variation between the precise and anticipated values is measured by the Imply Absolute Share Error (MAPE), which sheds gentle on the accuracy of the predictions of the magnitude of the particular worth. It’s calculated as:
$$start{aligned} textual content {MAPE} = frac{1}{n} sum _{i=1}^{n} left| frac{y_i – hat{y}_i}{y_i} proper| instances 100% finish{aligned}$$
(20)
the place, (y_i) denotes the precise worth, (hat{y}_i) the anticipated goal worth of the (i^textual content {th}) pattern, (n) the variety of samples.